Contoh soal dan jawaban Fungsi Aljabar Limit
Penyelesaian (a) :
Lim = (3x - 3) sin (x² + x - 2)
x → 1 tan² (2x - 2)
= 3 (x - 1) sin (x - 1) (x + 2)
tan² 2(x - 1)
= 3 (x - 1) * sin (x - 1) (x + 2)
tan 2(x - 1) tan 2(x - 1)
= 3 * (x + 2) = 3 * 3 = 9
2 2 2 2 4
Hasil = 9/4
Penyelesaian (b) :
Lim = tan (πx - 2π)
x → 2 2x - 4
= tan π (x - 2) = π
2 (x - 2) 2
Hasil = π/2
Contoh soal 2 :
Penyelesaian :
Lim = x² + 2x + 4
x → 2 x² - 6x + 2
= 2² + 2 (2) + 4
2² - 6 (2) +2
= 12 = -2
-6
Hasil = -2
Contoh soal 3 :
Lim = 5x⁴ - 6
x → 0 2x² - 1
Penyelesaian :
Lim = 5x⁴ - 6
x → 0 2x² - 1
= x (4x ³ - 6) = 4x³ - 6
x (2x - 1) 2x - 1
= 4 (0)³ - 6 = 0 - 6
2 (0) - 1 0 - 1
= 6
Hasil = 6
Contoh soal 4 :
Lim = (2x - 5x)(3 + (√9 + x)
x → 0 (9 - (9 + x))
Penyelesaian.
Lim = (2x² - 5x)(3 + √(9 + x))
x → 0 (9 - (9 + x))
= x (2x - 5)(3 + √(9 + x))
(9 - 9 - x)
= x (2x - 5)(3 + √(9 + x))
- x
= -(2x - 5)(3 + √(9 + x))
= -(2*0 - 5)(3 + √(9 + 0))
= 30
Hasil = 30
Contoh soal 5 :
Penyelesaian (1) :
Lim = 4x - sin 2x
X → 0 3x + tan x
4x - sin 2x
= x x
3x + tan x
x x
= 4 - 2 = 2 = 1
3 + 1 4 2
Hasil = 1/2
Penyelesaian (2) :
Lim = 4 sin 3x
x → 0 3 sin 6x
= 4 = Lim = sin 3 x = 4 * 3
3 x → 0 sin 6 x 3 6
= 4 = 2
6 3
Hasil = 2/3
Penyelesaian (3) :
Penting = sin 2x cos 2x = ½ sin 4x
Karena = sin 4x = 2 sin 2x cos 2x
Lim = 2x sin 2x cos 2x
x → 0 tan²x
= 2x * ½ sin 4x = x sin 4x
tan²x tan²x
= x * sin 4x = 1 * 4 = 4
tan x tan x
Hasil = 4
Penyelesaian (4) :
Lim = x² + 2x - 8
x → 2 3x sin (2 - x)
= (-4 - x)(2 - x) = -4 + x
3x sin (2 - x) 3x
= - 4 + 2 = -6 = 1
3 * 2 6
Hasil = 1
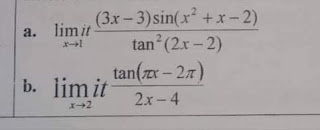

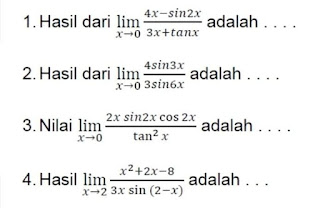



Komentar
Posting Komentar